Startseite    
MathematikPoolNRW Projekt Hintergründe Kontakt


Das Minimierungsproblem

Eine Funktion $f$ von $n$ unabhängigen Veränderlichen $x_1,...,x_n$ ist eine Vorschrift, die jedem $n$-Tupel reeller Zahlen (d.h. jeder Kombination von $n$ vielen reellen Zahlen) genau eine reelle Zahl $r=f(x_1,...,x_n)$ zuordnet.

Beispiel:
Für die Funktion

        $f(x_1,x_2,x_3)=3x_1x_2+2x_1+x_3$
ist

        $f(1,2,5)=3\cdot 1\cdot 2 + 2\cdot 1 +5=13$

Wir wollen nun für eine gegebene Funktion $f$ dasjenige $n$-Tupel $\vec{x}^{\ *}=(x_1^*,...,x_n^*)$ bestimmen, das $f$ minimiert, d.h. es soll gelten
$f(x_1^*,...,x_n^*) \le f(x_1,...,x_n)$ bzw. $f(\vec{x}^{\ *}) \le f(\vec{x})$
für alle übrigen $n$-Tupel $\vec{x}=(x_1,...,x_n)$.

Beispiel:
Das Minimum der Funktion

        $f(x,y)=x^2+y^2+xy+2x-1$

ist $(x^*,y^*)=(-\frac{4}{3},\frac{2}{3})$, denn es gilt
       $f(-\frac{4}{3},\frac{2}{3}) = -\frac{7}{3} \le f(x,y)$ für alle reellen Werte $x,y$,
wie wir in den folgenden Abschnitten beweisen werden.

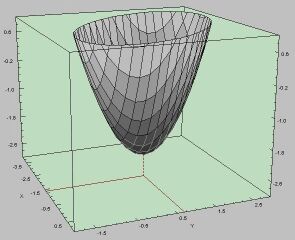Das Minimum $\vec{x}^{\ *}$ lässt sich mit dem konjugierten Gradientenverfahren bestimmen.
Wir werden uns auf differenzierbare Funktionen in $n=2$ Veränderlichen beschränken.