Startseite    
MathematikPoolNRW Projekt Hintergründe Kontakt


Quadratische Funktionen

Im folgenden schreiben wir abkürzend ${\vec{a}}$ für das Tupel $(a_1,a_2)$ und $Q$ für die Matrix
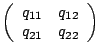$ \left( \begin{array}{cc} q_{11}& q_{12}\cr q_{21} &q_{22} \end{array} \right) $ .
Bei der symmetrischen Matrix sind alle Elemente spiegelbildlich zur Hauptdiagonalen angeordnet, d.h. $Q$ ist symmetrisch, falls $q_{12} = q_{21}$ gilt.
Weiter bezeichne
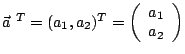
$ \vec{a}^{\ T} = (a_1,a_2)^T = \left( \begin{array}{c} a_1\cr a_2 \end{array} \right) $
das zu $\vec{a}$ transponierte (,,umgedrehte ``) Tupel und $c_1$ eine feste Zahl.

Eine Funktion $f$ heisst quadratisch, wenn es eine symmetrische Matrix $Q$, einen Vektor $\vec{a}$ und eine reelle Zahl $c_1$ gibt mit der Eigenschaft
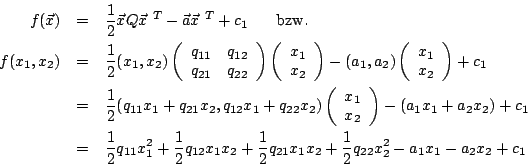
\begin{eqnarray*} f(\vec{x})& =& \frac{1}{2} \vec{x} Q \vec{x}^{\ T} - \vec{a}... ...}{2}q_{21}x_1x_2 + \frac{1}{2}q_{22}x_2^2 -a_1x_1 -a_2x_2 +c_1 \end{eqnarray*}

 
Beispiel:
Die Funktion

        $f(x,y)=x^2+y^2+xy+2x-1$
hat die Gestalt

        $ f(\vec{x})= \frac{1}{2} \vec{x} \left( \begin{array}{cc} 2& 1\cr 1&2 \end{array} \right) \vec{x}^{\ T} - (-2,0)\vec{x}^{\ T} + (-1) $.

Für den Gradienten einer quadratischen Funktion $f$ ergibt sich
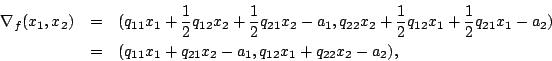
\begin{eqnarray*} \nabla_f(x_1,x_2) &=& (q_{11}x_1+\frac{1}{2}q_{12}x_2+\frac{... ...a_2) \\ &=&(q_{11}x_1+q_{21}x_2-a_1,q_{12}x_1+q_{22}x_2-a_2), \end{eqnarray*}

d.h. der Gradient ist $\nabla_f(\vec{x}) = \vec{x}Q - \vec{a}$.

Für die Hessematrix einer quadratischen Funktion $f$ errechnet man
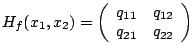$ H_f(x_1,x_2)= \left( \begin{array}{cc} q_{11}& q_{12}\cr q_{21}& q_{22} \end{array} \right) $,
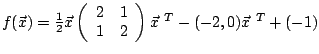d.h. die Hessematrix ist $H_f(\vec{x})= Q$.