Als Abstraktion eines Verkehrsnetzes, das aus Bahnhöfen, Städten oder Kreuzungen und Gleis- oder Straßenverbindungen besteht, verwenden wir Graphen.

Ein gerichteter Graph besteht aus

• einer (endlichen) Menge V von Knoten und
• einer (endlichen) Menge E von Kanten,

die je zwei Knoten miteinander verbinden. Wir können daher E mit einer Teilmenge { (v,w) aus V } identifizieren. Zusätzlich seien nichtnegative ''Entfernungen'' c(v,w) >= 0  gegeben und ein Startknoten s aus V ausgezeichnet.

Wir veranschaulichen uns Graphen, indem wir die Knoten als kleine Kreise zeichnen und die Kanten (v,w) als Pfeile, die einen Knoten v mit einem Knoten w verbinden.


Beispiel:

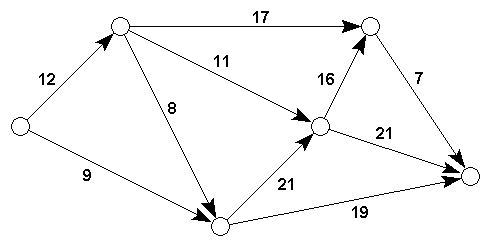
Unter einem Weg   P   von einem Knoten   v   zu einem anderen Knoten   w   verstehen wir eine Folge   v₀, v₁, ... , v_k   von Knoten, so daß   v₀ = v,  v_k = w   und   (v_i, v_i+1) Kanten aus   E  sind. Der Weg hat die Länge

c(P) = c(v₀,v₁) + c(v₁, v₂) + ... + c(v_k-1,v_k).

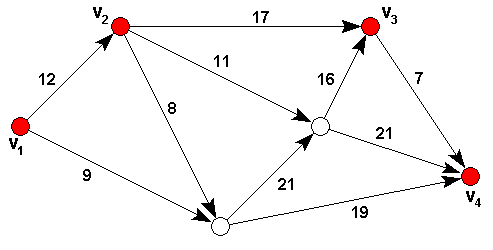
Beispiel:    In dem folgenden Graphen führt der Weg P von Knoten v₁ über die Knoten v₂ und v₃ nach v₄.
                  Er hat die Länge


Das kürzeste-Weg-Problem besteht darin, Wege kürzester Länge von s zu einem ausgezeichneten Zielknoten t bzw. zu allen anderen Knoten zu bestimmen.

---